Google spotlights the quadratic equation with a new Doodle and learning tools — why it’s trending today and how to use it

Bassyonni

ago 1 month

quadratic equation

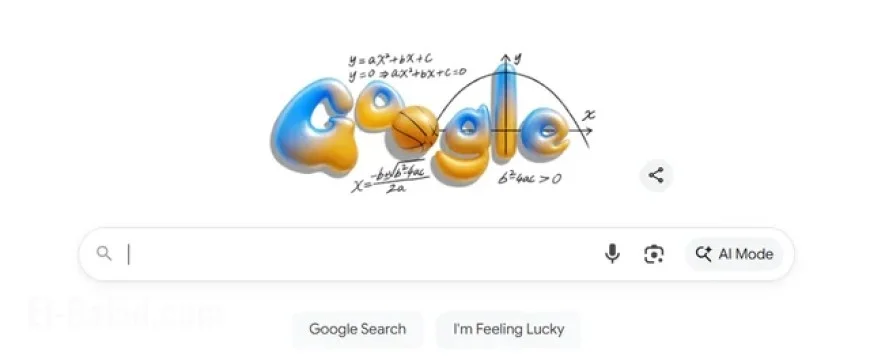
The quadratic equation is having a moment. A new animated homepage Doodle rolling out today across parts of Europe, the Middle East, and Africa turns the iconic logo into a quick lesson on ax² + bx + c = 0, reminding students—and plenty of adults—how to solve parabolas with the quadratic formula. The back-to-school-themed artwork follows last month’s debut in the U.S. and U.K., extending the campaign to more regions just as midterm exams approach.

What the Doodle teaches in 10 seconds

The animation walks through the essentials: identify a, b, c in a standard-form quadratic; plug them into the formula; visualize the curve’s roots where it crosses the x-axis. It’s a bite-size refresher designed to nudge learners into deeper practice with calculators, lessons, and interactive help that sit one click away from the homepage.

Quick refresher you can screenshot

Standard form: ax² + bx + c = 0 (with a ≠ 0)
Quadratic formula: x = [-b ± √(b² − 4ac)] / (2a)
Discriminant (Δ = b² − 4ac) tells you how many real solutions:
- Δ > 0 → two real roots
- Δ = 0 → one real root (a double root)
- Δ < 0 → no real roots (complex pair)

Why the quadratic equation is suddenly trending

Curriculum timing: Many school systems hit quadratics in October–November; searches spike as classes shift from linear to polynomial models.
Study features in Search: Students can type or speak “quadratic equation,” scan problems from paper, and get step-by-step guidance with explanations, graphs, and practice variants.
Visual hooks: Parabolas map to real life—projectile motion, satellite dishes, even “smile vs. frown” lenses—making them perfect candidates for a visual Doodle.

How to solve one fast (worked example)

Solve 2x² − 5x − 3 = 0

a = 2, b = −5, c = −3
Δ = b² − 4ac = (−5)² − 4(2)(−3) = 25 + 24 = 49
x = [5 ± √49] / 4 = [5 ± 7] / 4
- x₁ = (5 + 7)/4 = 12/4 = 3
- x₂ = (5 − 7)/4 = −2/4 = −½

Two clean roots: x = 3 and x = −0.5. (Notice how a perfect-square discriminant produced rational answers.)

Tips for students using Search and camera tools

Standardize first: Rearrange your problem into ax² + bx + c = 0 before scanning or typing; you’ll get cleaner, step-by-step output.
Check units & context: In physics problems (e.g., ballistics), label units and confirm whether time or height is the unknown—then pick the root that makes physical sense (negative time often isn’t).
Graph to verify: A quick plot confirms where the curve crosses the x-axis and whether your answers match the intercepts.
Mind rounding: Keep at least 3–4 significant figures until the final step to avoid off-by-a-little errors.

Classroom angles: making parabolas stick

Discriminant drills: Rapid-fire Δ classification builds intuition about root counts before you ever compute them.
Vertex form bridges: After solving, convert to a(x − h)² + k to read the vertex and symmetry; it cements the link between algebra and geometry.
Model a story: Fit a simple projectile dataset to a quadratic, then interpret the intercepts (launch/landing), vertex (maximum height), and axis of symmetry (mid-flight time).

Why this matters beyond homework

Quadratics are the gateway to more advanced math: optimization in calculus, curve fitting in data science, potential wells in physics, even pricing models in finance. Pairing a playful Doodle with robust problem-solving tools lowers the friction for learners who might otherwise bounce off the first square root.

Today’s Doodle isn’t just a cute animation—it’s a well-timed study nudge. If “quadratic equation” is on your syllabus, use the momentum: standardize the problem, apply the formula, check the discriminant, and graph to verify. With midterms looming, that 10-second homepage lesson can be the doorway to mastering one of math’s most useful workhorses.